Numerical Aperture , Resoving Power , Depth of Focus

이제, 개구수(Numerical Aperture), 분해능(Resolving power), 심도
(Depth of Focus)에 대한 설명으로 넘어 가겠습니다.

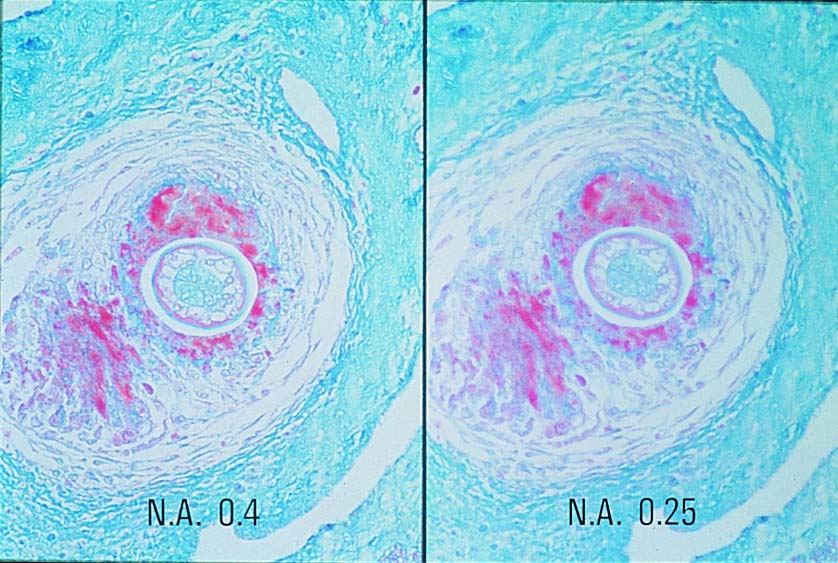
이론상으로 확대율은 거의 무한하게 증가될 수 있지만 만약 확대했을 때 이미지가 선명하지 않으면 그것은 의미가 없는 것이라 할 수 있습니다. 이미지의 선명함을 결정하는데 있어 중요 요인으로 꼽히는 것은 대물렌즈의 분해능입니다. 이 분해능은 대물렌즈의 개구수(N.A)에 의해 결정됩니다.

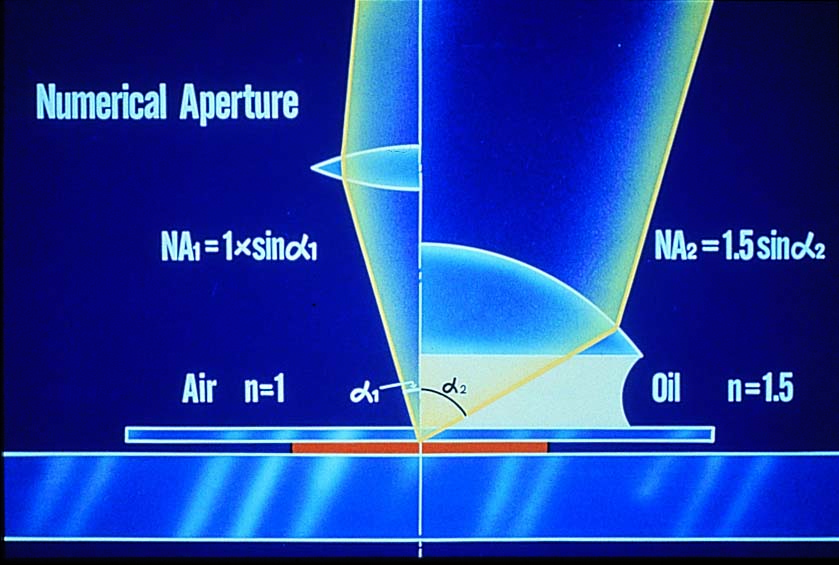
개구수(N.A)는 실제로 대물렌즈의 밝기와 분해능에 영향을 주고, 카메라 렌즈의 조리개값(F-number)으로 이해 할 수 있습니다. 개구수는 표본과 대물렌즈 사이 물질의 반사지수를 나타내는 상수값 n과 그 각도 α의 sine값에 의해 결정됩니다. 건식(Dry)타입은 매개물질이 공기이므로 굴절율 1을 갖습니다. 반면에 오일타입의 대물렌즈는 대개 굴절율 1.515와 같은 값을 가진다. α는 대물렌즈의 광학축을 기준으로 기울어진 광원의 입사 각도입니다.

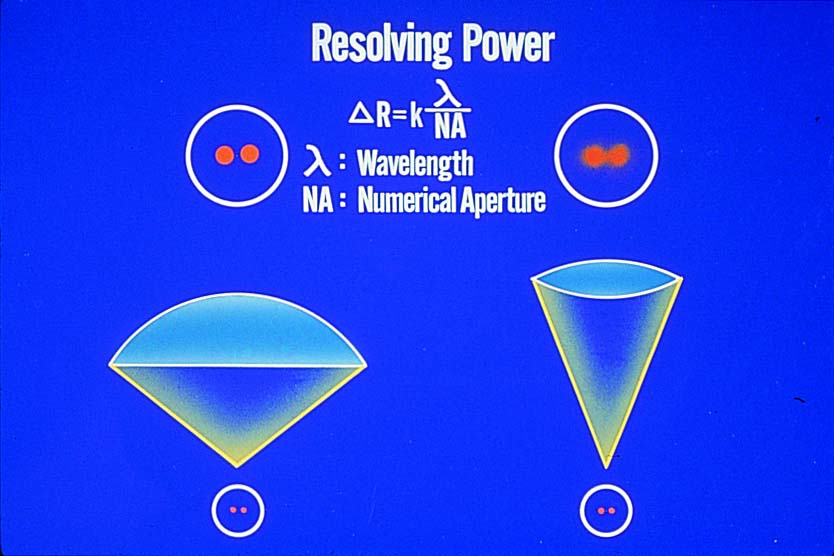
이런 까닭에 개구수(N.A)는 대물렌즈의 분해능에 큰 영향을 미칩니다. 분해능의 두 점을 두점을 두 점으로 인식할 수 있는 최소 거리입니다.

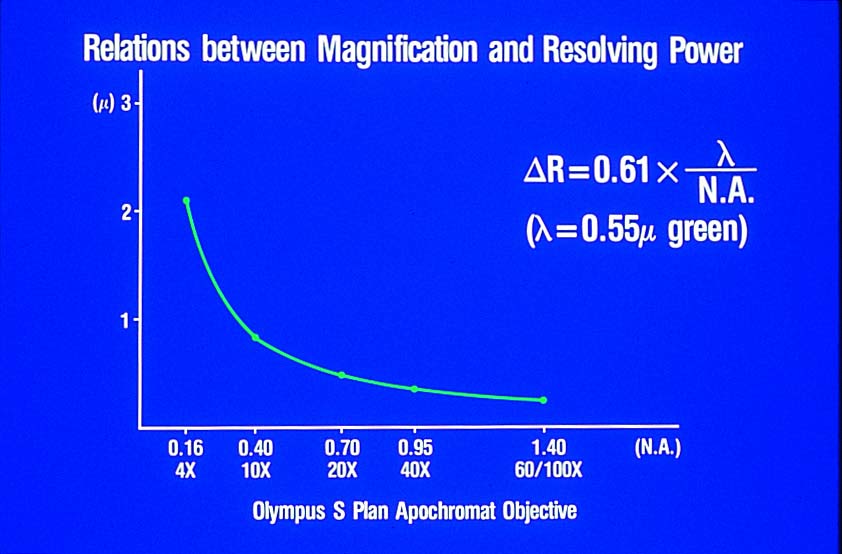
우리가 두 점 사이의 분해거리(resolved distance)를 ∆R이라 부른다면, 여기서 λ는 빛의 파장길이, K는 상수이다. 파장 변화가 없는 상태에서 개구수 값을 올리면 보다 작은 ∆R값을 얻을 수 있다. 광학 현미경의 최소 분해한계 거리는 대략 0.25㎛ 입니다.

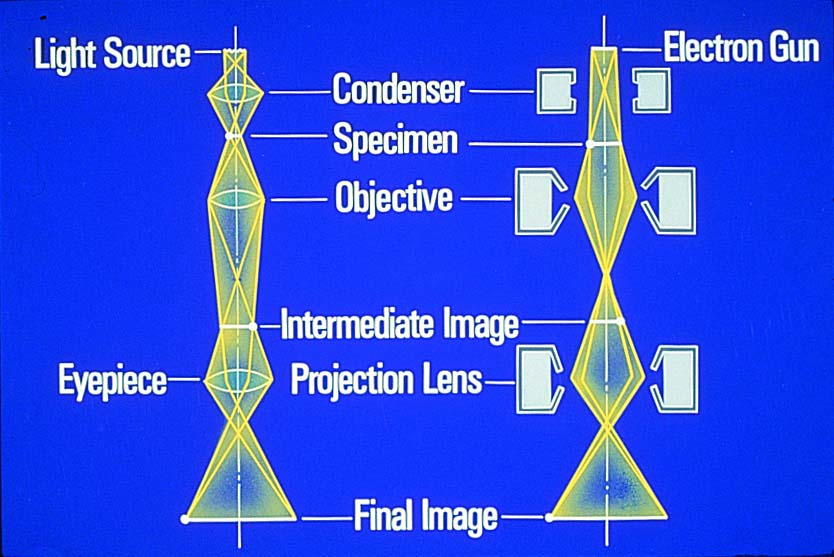
개구수(N.A.)값의 증가는 한계가 있으므로 빛보다 짧은 파장의 전자빔을 이용, ∆R값을 보다 감소시킬 수 있다. 이 이론이 광학현미경보다 1000배 이상의 분해능을 가진 전자현미경의 원리이다. 그러나 전자현미경은 살아있는 표본 관찰이 어렵고, 표본을 준비하는데, 전처리가 필요하며, 염색할 수가 없고 가격이 매우 비싼편에 속합니다. 이런 이유로에 광학현미경과 전자현미경은 상호보완적으로 사용되어 지고 있습니다.

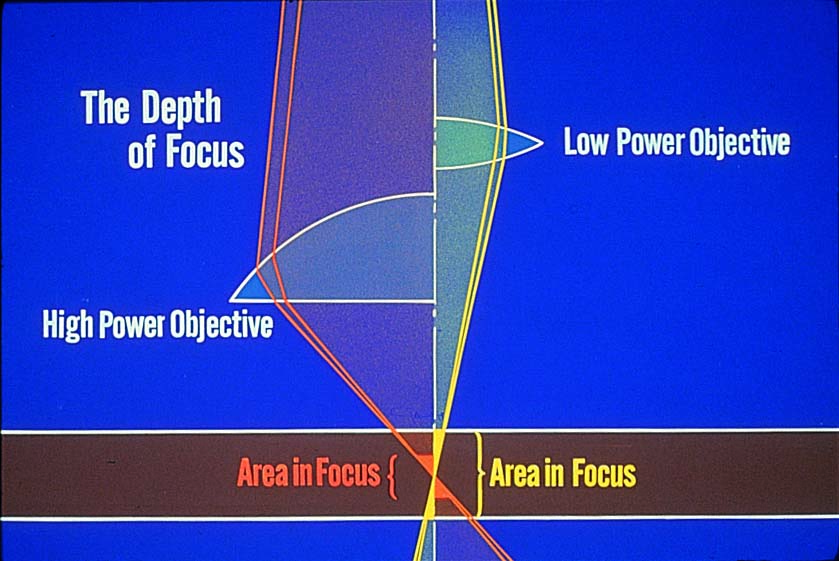
현미경 설계에서 중요한 다른 요소는 한번에 초점을 잡을 수 있는 최대깊이인 초점의 심도(depth of focus)입니다. 보다 큰 초점 심도는 두꺼운 표본의 관찰을 용이하게 합니다. 그러나 초점심도는 대물렌즈의 배율과 개구수에 반비례한 특성이 있습니다. 따라서, 배율과 분해능이 커질수록 심도는 얇아진다는 것을 의미합니다.